Master thesis of Britt Cordewener

Composite materials are engineered materials consisting of two or more constituents with different physical and/or chemical properties that remain separate and distinct in the finished material. In Fiber Reinforced Composites (FRC), the continuous phase is referred to as the matrix of which the properties are enhanced by adding either long or short fibers (continuous or discontinuous FRC, respectively). Their application within the engineering field has increased substantially over the last few years due to their excellent mechanical properties and weight saving ability. For most fiber composites, however, the compressive strength is substantially less than their tensile strength, causing it to be a design limiting feature in many applications. Therefore, the compressive failure of composite materials has been the subject of extensive previous research. Several competing failure modes have been identified, among which the micro-buckling of fibers.

In Fiber Reinforced Composites (FRC), fibers of high strength and modulus are embedded in or bonded to a matrix while a distinct interface remains between them. The fibers are considered as the principal load-carrying constituents, whereas the surrounding matrix acts mainly as a load-transferring medium between the fibers and a binder to maintain the shape of the product and orientation of the fibers.

Though extensive research in the past has resulted in significant improvements to the tensile strength, impact resistance and toughness, the longitudinal compressive performance of Fiber Reinforced Composites has not been increased. For unidirectional carbon fiber epoxy composites, for example, their compressive strength equals approximately 50 to 60% of their tensile strength.

Elastic micro-buckling, plastic micro-buckling, fiber crushing, splitting, buckle delamination and shear-band formation are regarded as the main competing mechanisms of compressive failure of unidirectional long fiber composites. The governing mode appears to be strongly correlated with the shear properties of the matrix and the gradation of initial imperfections such as the fiber misalignment. While having low shear strengths, micro-buckling - the localized buckling of fibers in a cooperative manner - is observed as the compressive failure of unidirectional polymer-matrix composites. Depending on whether the matrix behaves in an elastic manner or shows plastic deformation, either elastic or plastic micro-buckling of the fibers is observed. The latter occurs at sufficiently large strains for the matrix to deform in a non-linear manner. At highly localized areas in which fibers are initially misaligned from the loading direction, fiber bundles rotate or tilt from their initial configuration, causing large shear deformation in the surrounding matrix and so-called kink bands. In case of an elastic behavior of the matrix, elastic micro-buckling of the fibers is observed. On a micro-scale, the individual slender fibers can buckle in two distinct micro-buckling patterns; either in transverse (out-of-phase) buckling or in shear (in-phase) buckling mode, causing the matrix to undergo extensional straining in transverse direction or shearing parallel to the fibers respectively.

The bifurcation load of an individual slender fiber embedded in a matrix can be computed using a Winkler foundation model as proposed in the early models of Rosen (1965). Fibers are approached as being perfectly aligned elastic and slender columns supported by an elastomeric matrix, which is simplified as an array of springs with continuous spring stiffness or foundation modulus Kc, see Figure 1. The differential equation for a fiber on an elastic foundation loaded by a point load is then found to be:

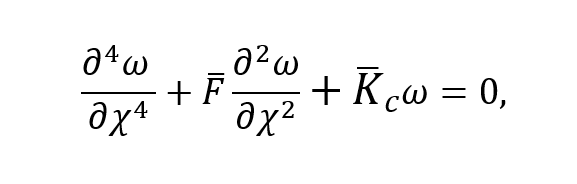
where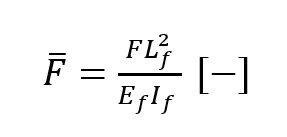and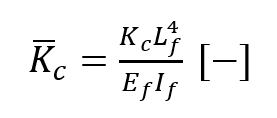are the dimensionless compressive force and continuous spring stiffness of the matrix respectively, with the fiber’s Young’s modulus Ef , length Lf and second moment of area If , the normalized displacement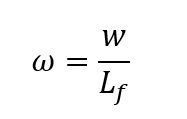and the position along the beam axis.

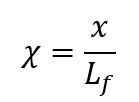Figure 1: Individual fiber embedded in a matrix as approached by the Winkler model and discretized using DEM

For a fiber of which both ends are free to rotate and restricted against lateral displacements the analytical solution is found to be:

The critical buckling force can be found upon calculation of the mode number n that minimizes the solution for the compression force. The result is shown in Figure 2. The governing buckling mode increases with increasing continuous spring stiffness representing the matrix. In contrast to fibers not embedded in a matrix, the critical buckling load does not decrease monotonically with increasing fiber length. Instead, the governing buckling mode with corresponding number of half waves becomes highly sensitive to small heterogeneities in the bending stiffness of the fiber, the fiber length and the foundation modulus of the matrix.

To evaluate the influence of material properties on the micro-buckling of individual fibers, a numerical model using the Discrete Element Method (DEM) is created. The load displacement diagram of a fiber under compressive loading is obtained by a non-linear buckling analysis based on the principle of stationary total potential energy, using a standard Newton-Raphson procedure.

To evaluate the influence of the matrix on the critical buckling load, two ways to compute the foundation modulus of the matrix have been adopted. Following Su et al. (2014), the continuous spring stiffness is computed using Kelvin's solution for the displacement field of an infinite unbounded elastic medium subjected to a concentrated force.

Alternatively, a simplified approximation for the continuous spring stiffness is computed using merely the Young's modulus of the matrix. It is concluded that the value of the spring stiffness is linearly dependent on the matrix-fiber stiffness ratio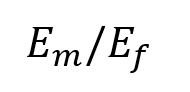. The difference between the buckling forces obtained with both methods is found to be independent of the fiber aspect ratio and merely depends on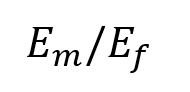. For low values of the matrixfiber stiffness ratio, the difference is sufficiently small, allowing for the application of the more simple approximation of the foundation modulus by.

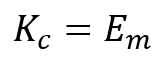Plasticity of the matrix is included using a bilinear material model. The stiffness of the springs representing the matrix support is adapted using reduction factor α as soon as the matrix starts to yield. Depending on the moment at which the displacement corresponding to the onset of plastic matrix behavior is reached, matrix plasticity influences either the critical buckling load, or merely the post-buckling behavior of the fibers. When combined with fiber plasticity, plastic matrix behavior causes the fibers eventually to fail in plastic microbuckling and the initiation of fiber kinking is observed, see the left figure above the title.

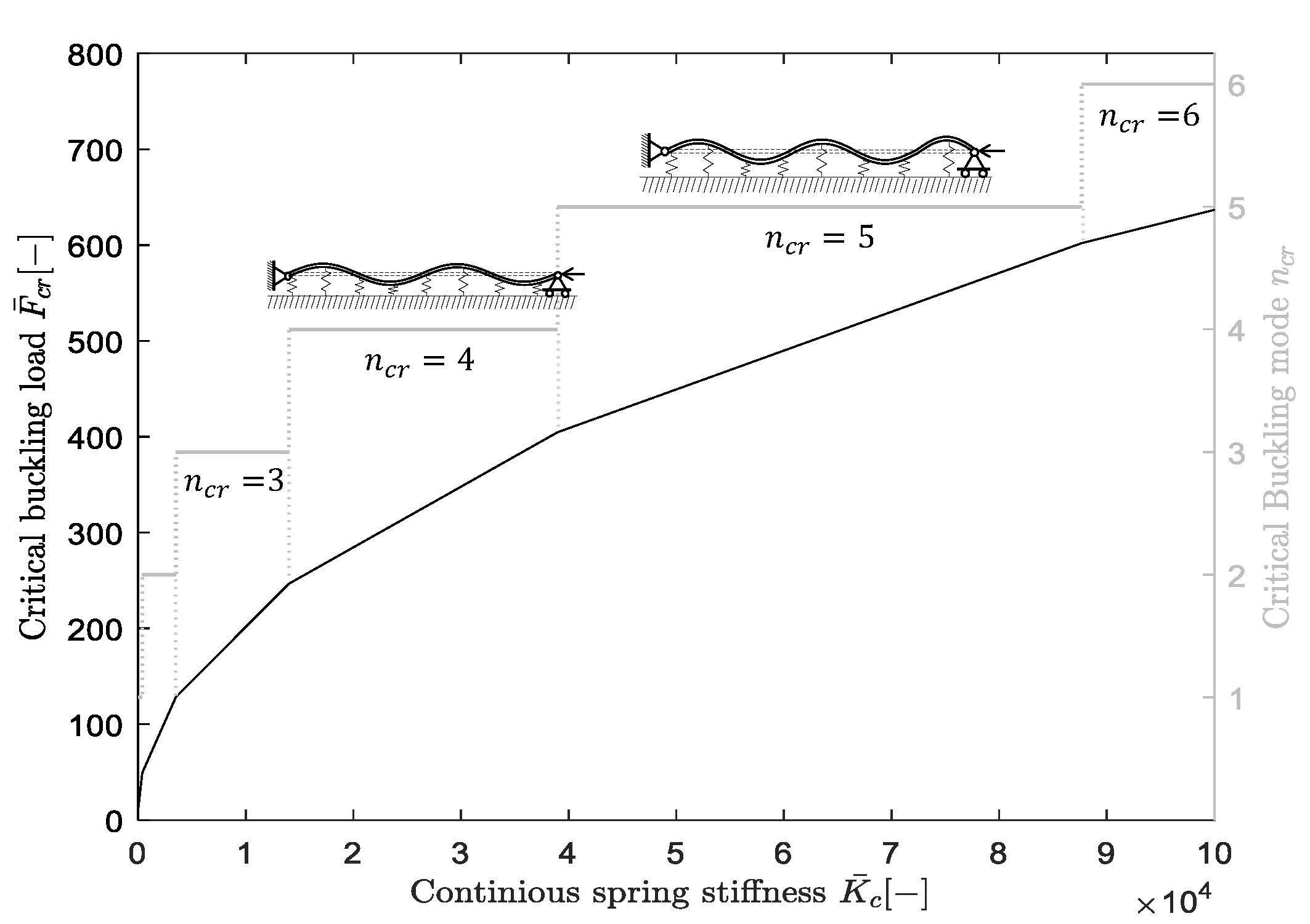
Figure 2: Analytical buckling load and mode of an individual embedded fiber as a function of the foundation modulus of the matrix.

A model for fiber bundles embedded in a matrix is constructed and used to evaluate the influence of initial imperfections and fiber volume fractions on the buckling behavior of fibers. Besides the original springs representing the support of the matrix, coupling springs connecting adjacent fiber nodes are introduced to capture the fiber-matrix interaction correctly. The fiber volume fraction (vf ) of the composite material is accounted for by reduction functions. It is observed that for low fiber volume fractions, fibers may buckle out of phase (transverse mode), depending on their initial imperfections and misalignment. For composites with high fiber volume fractions, the limited distance between adjacent fibers causes the fibers to buckle in phase (shear mode), despite their possibly in opposite direction imposed initial imperfections, see the right figure above the title which shows the displacement of 5 fibers in a bundle evolving under increasing compressive loading.

Though extensive experimental calibration is still required, the created DEM models are able to describe the elastic microbuckling of embedded fibers accurately and can be used to quickly increase the insight into various relations between fiber behavior and material parameters of composites.