The Onyx Tower
A while ago, we gave a KOers lunchlecture about the newest high-rise tower in Eindhoven: the Onyx tower. During this lecture, a lot of aspects about the building and design process of a tower in the city center of Eindhoven were treated; we paid special attention to the different parties involved in this process and their interests herein. Although many students attended and were interested, the main criticism we received from them was that they would like to know more about the structural mechanics behind such a building. We took this to heart and will not fill this article with all kinds of facts about Onyx, we will write about its structural mechanics in relation to the second order effect.
A lot can be written about the statics of such a tall building, in fact, too much for an article this size. Therefore, the subject treated in this article will deal with a phenomenon that required our attention at the start of the design process; what is the size of the nth-order effect of a high-rise and how can it be determined.
We often see that determining the nth-order factor, e.g. the amplification of the first order elastic deformation due to axial forces in a structure, is easily dismissed with “n/n-1< 1.1, no further analysis needed”. When the nth-order effect is smaller than 1.1 it can be ignored according to our design codes. The reasoning behind this is that if this factor is smaller than 1.1 the effect of amplifying the first order internal forces is small, so small that it is not necessary to perform complex geometrically nonlinear analyses. The complexity in determining n/n-1 is discussed later on.
When n/n-1 is larger than 1.1, it is often necessary to perform these complex analyses for buildings such as the Onyx tower. The difficulty in this is that, unlike the results of linear-elastic analysis, results from different load combinations are not interchangeable. Each separate load combination, e.g. permanent load and live load or permanent load and wind, must be calculated and analyzed separately. This increases both the amount of results to be analyzed and the time needed by an engineer to analyze the results properly. If the results lead to an adaptation in the structural design, the whole process starts over again.

Figure 1: Simple schematization of a high-rise structure
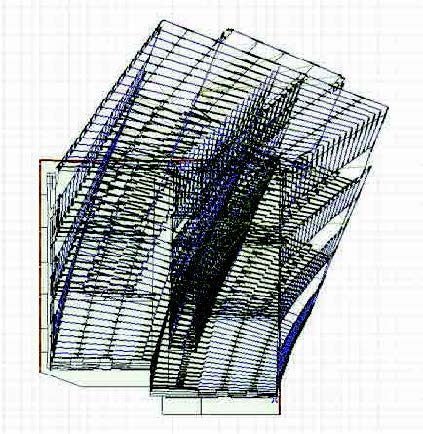

Figure 2: Deformation of the 3D FEM-model
Consequently, during the design and progressive calculation phases, engineers try to avoid the necessity of nonlinear analyses. This is not because engineers are ‘work-shy’, the design and calculation of a high-rise is complex enough as it is. The design process has many different parties with each their own interests, leading to many changes in the design. As a structural engineer, all available time is needed in this phase to control for structural integrity. If too much time is spent on ‘perhaps unnecessary complex analyses’, the control over the structural integrity can be easily lost. However, this is a subject we dealt with during the lunch lecture, back to structural mechanics.
The first few floors of the Onyx tower are made of in-situ concrete. From the second floor up, the walls are made of precast concrete elements. Each floor contains 37 different (21 interior and 16 facade) precast interlocking wall-to-wall elements. A building constructed of precast elements is quickly put together. However, the internal forces now have to be analyzed for 24 floors made of 37 elements each, which is 888 elements in total, instead of 6 or 7 shear walls. Therefore, it was chosen to calculate and analyze the entire structure in one Finite Element Method model (FEM-model) using shell, connection, and beam elements. This way, the distribution of internal forces of the foundation, basement, first floors, and the entire precast concrete structure could be analyzed as a whole.
If geometrically nonlinear analyses are to be avoided, it is necessary to determine the magnitude of n/ n-1. Due to the complexity of the building structure, this cannot be approximated through simple statics. In a simple statics scheme, the tower is assumed to be a cantilever beam with a rotational spring at the base to account for the stiffness of the foundation. The second order effect can then be calculated with:
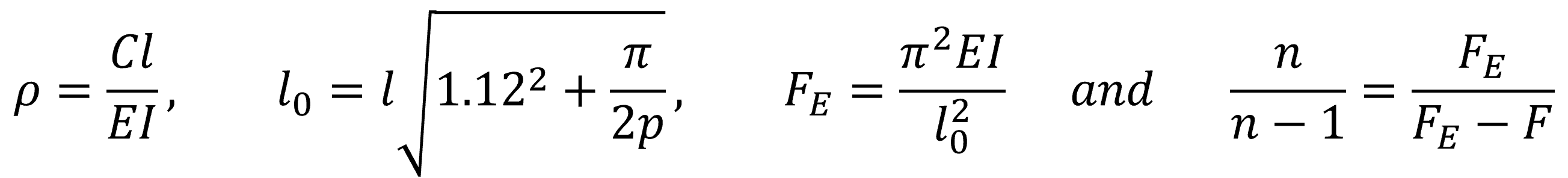
In the above, it is assumed that the total structure can be calculated according to the schematization in Figure 1. For multiple buildings of the size of Onyx we have found that the deformation is similar to the one shown in Figure 1.
After the results of the 3D FEM-model were analyzed, we found that the calculated deformation deviated in two ways from the scheme in Figure 1, see Figure 2. The first deviation is the deformation of the foundation slab supporting the tower in combination with the column-beam-wall structure in the lower part of the building. This deformation, see Figure 3, cannot be described by the rotational spring at the base in Figure 1. The second deviation is found in the deformation of the tower. On top of deformation due to bending forces, shear deformation and rotation of the tower are found, see Figure 3.
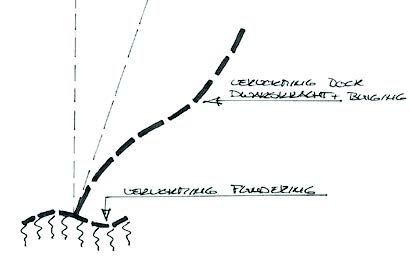
Figure 3: Deformation due to foundation stiffness, shear, and rotation
With these additional deformations the schematization in Figure 1 cannot fully describe the mechanical behavior of the complete structure. Therefore, we determined an alternative way to determine the value of n/n-1 for the Onyx tower.
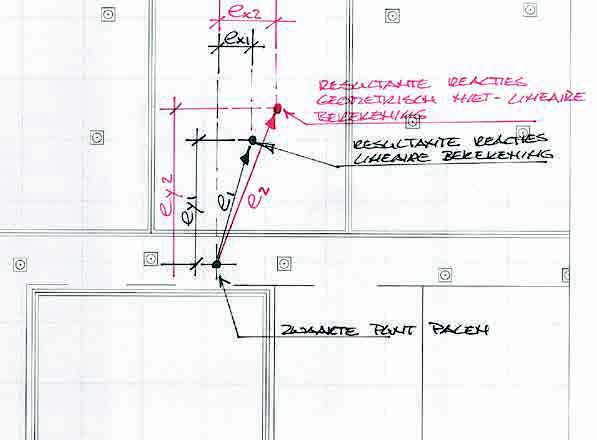
Figure 4: Shift of the center of gravity
A geometrically linear and nonlinear calculation were performed for the Onyx tower for the load combinations in which the deformations of the tower where most explicit, e.g. permanent and wind loads. The center of gravity of the pile foundation was compared to the center of gravity of the pile reactions for both the linear and nonlinear models. The resulting values can be termed e1 and e2. The n/n-1 factor is then found by e2 over e1:
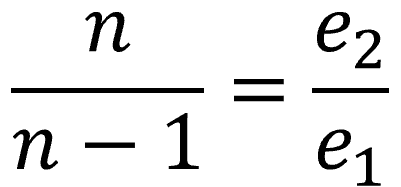
For the x- and y-directions the following was found:
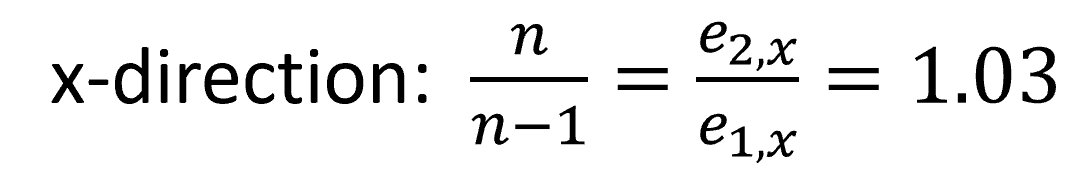
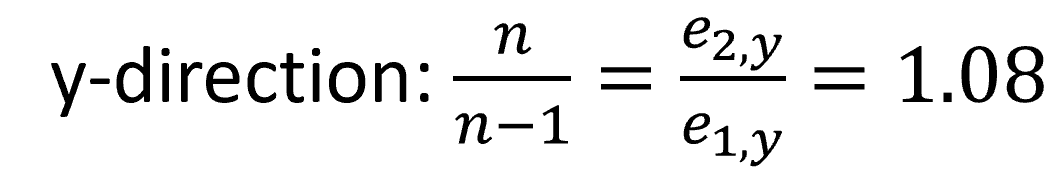
In conclusion, we proved through this analysis that the n/n-1 factor did not have to be applied and could be ignored in further calculations. This made the overall design process less complex and valuable time was gained, which could be used in design optimization.




