Master Thesis of Tomas Snel

The design process of a building can be described as “an iterative search process in which designers gather, generate, represent, transform, manipulate, and communicate information and knowledge related to various domains of design concepts” [1]. So, designers iterate over multiple design options and alternatives to find a design that meets all performance criteria to a satisfactory level. A correlation can be found between the amount of alternatives, or iterations, and the quality of the final chosen design [2], where a higher amount of alternatives correlates with a higher quality final design. Unfortunately, on average only three alternatives are considered in a normal design process. This is mainly due to the time constraints. Experts in the Architecture, Engineering, and Construction industry spend on average over a month to generate and evaluate a single design alternative [3]. This graduation project focuses on the rapid generation of early stage building spatial designs using a heuristic optimization approach. 

In previous research [4] and [5], a foundation has been developed to start the graduation project. Hofmeyer & Davila Delgado [4] developed a toolbox which includes representations, shown in Figure 1, of an early stage building design, a FEM implementation capable of calculating the structural performances,  and a procedures to optimize the structural performances. Boonstra et. al. [5] elaborated the toolbox and added a resistor-capacitor method to calculate thermal energy loss and developed evolutionary algorithms to optimize building spatial designs.

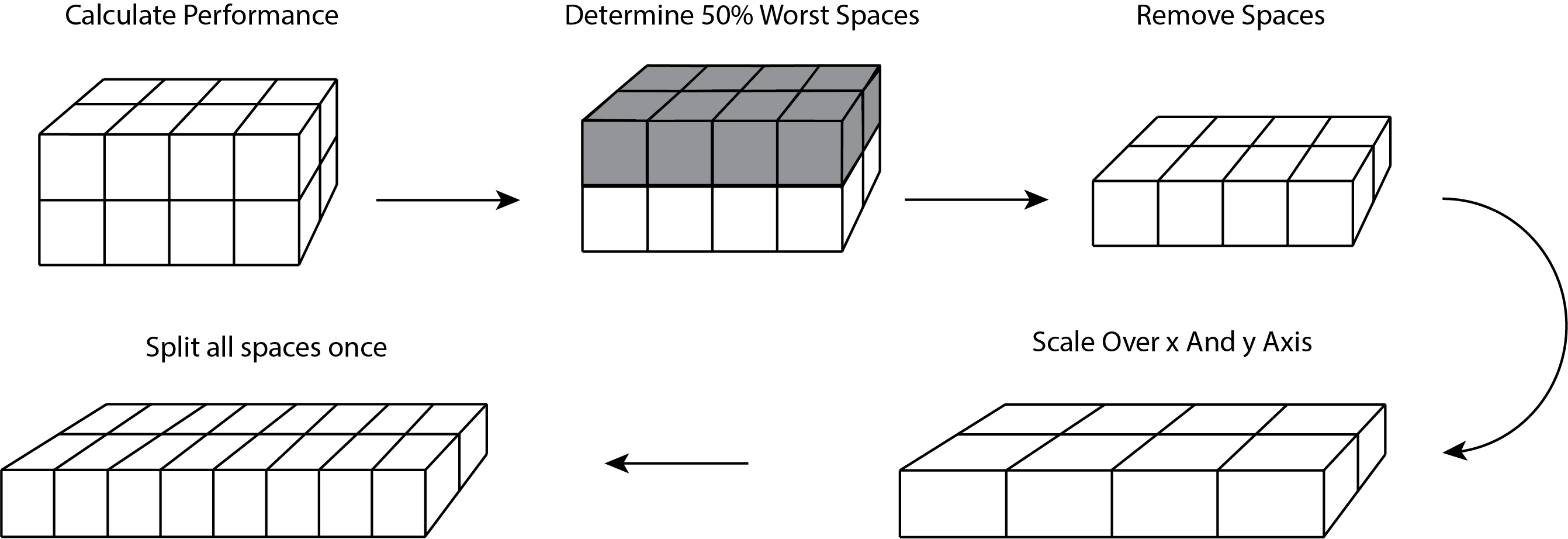
Figure 1: The initial heuristic procedure to optimize structural performances a building spatial design

It can be stated that the toolbox as mentioned in itself is not capable of optimizing designs. It only provides performance values of the design and the spaces within the design. The optimization is included in the evolutionary algorithms, which optimizes designs using the results from the toolbox. While evolutionary algorithms can be powerful, they have an intensive computation time. Hofmeyer & Davila Delgado [4] proved that heuristic algorithms outperform evolutionary algorithms when only a couple iterations are requested. 

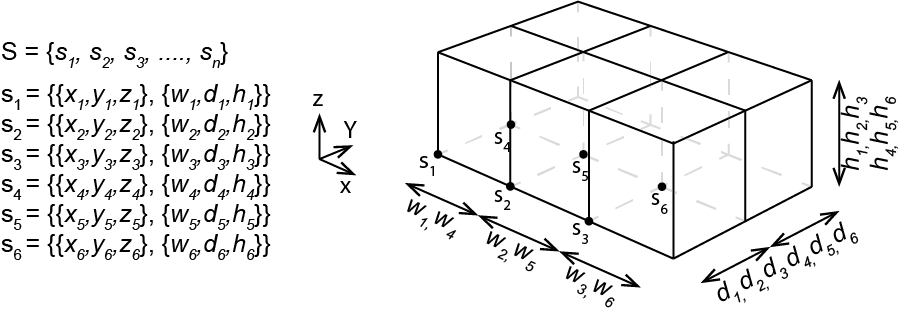
Figure 2: The building spatial design representation ‘Movable-Sizable’ as used for this study

Elaborating on the initial heuristic procedure and the aforementioned toolbox, an improved heuristic procedure is developed in C++, as shown in Figure 3. This research focuses on single disciplinary optimization, since the procedure should be capable of optimizing a single discipline before complex situation of multiple disciplines are introduced. Infrastructure and algorithms to apply multi-disciplinary optimizations are implemented for future research.

To generate new designs, the structural performance is defined as the total amount of strain energy and the building physics performance is defined as the thermal energy loss due to heating and cooling of spaces. The constraints for the procedure are set as follows: equal volume, equal space count, no overlap between spaces, and no floating spaces. 

The heuristic procedure in Figure 3 operates as follows: an initial design is required from which alternative designs are generated. The performances of the initial design are then calculated with the toolbox as developed by Boonstra et. al[5]. The following procedure is then divided into three sub-procedures: performance evaluation, space ranking, and building modification. For all stages, multiple parameters are developed and elaborated in order to interpret performances with different approaches, all resulting in different design solutions.

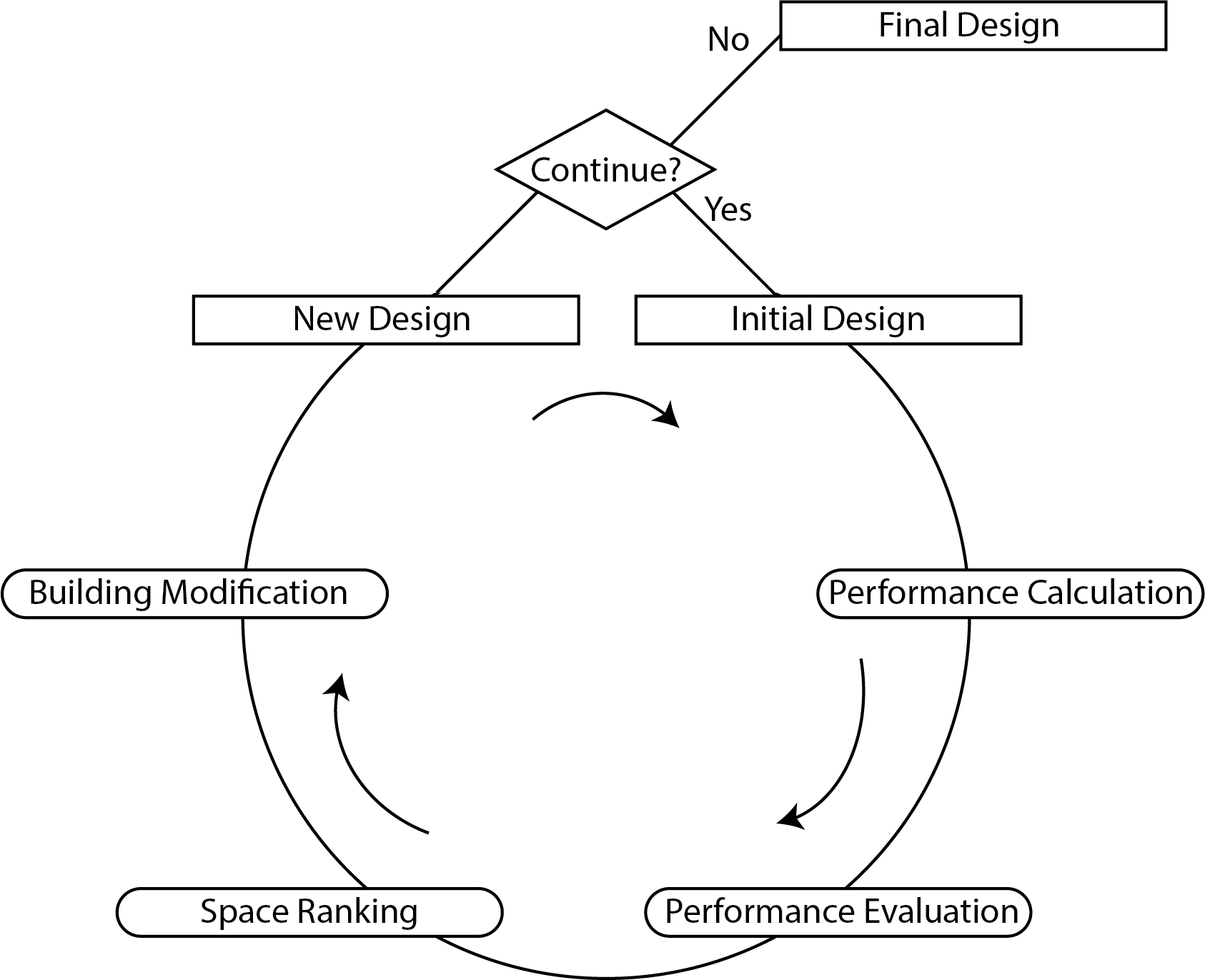
Figure 3: Heuristic Cycle as used in this study

The three sub-procedures are evaluated with a parameter study. This research shows that the procedure is capable of optimizing a building spatial design for either structural or building physics performance. For the performance evaluation procedure, it is shown that structural evaluation should rate spaces from best to worst as highest to lowest strain energy, as can be seen in Figure 4. Building physics evaluation should rate spaces from best to worst as lowest to highest thermal energy loss. Furthermore, it can be stated that combining a geometrical clustering approach with the evaluated performances is capable of improving a building spatial design for both disciplines. The space ranking in this study is straightforward since only one discipline is considered at a time. For the building modification sub procedure, the most effective parameters are those that move a building spatial design towards the most optimal shape for the given discipline. For structural optimization, this means a one storey high, square floor plan. Building physics optimization finds the best solutions when the modifications move the building spatial design towards a cuboid design.

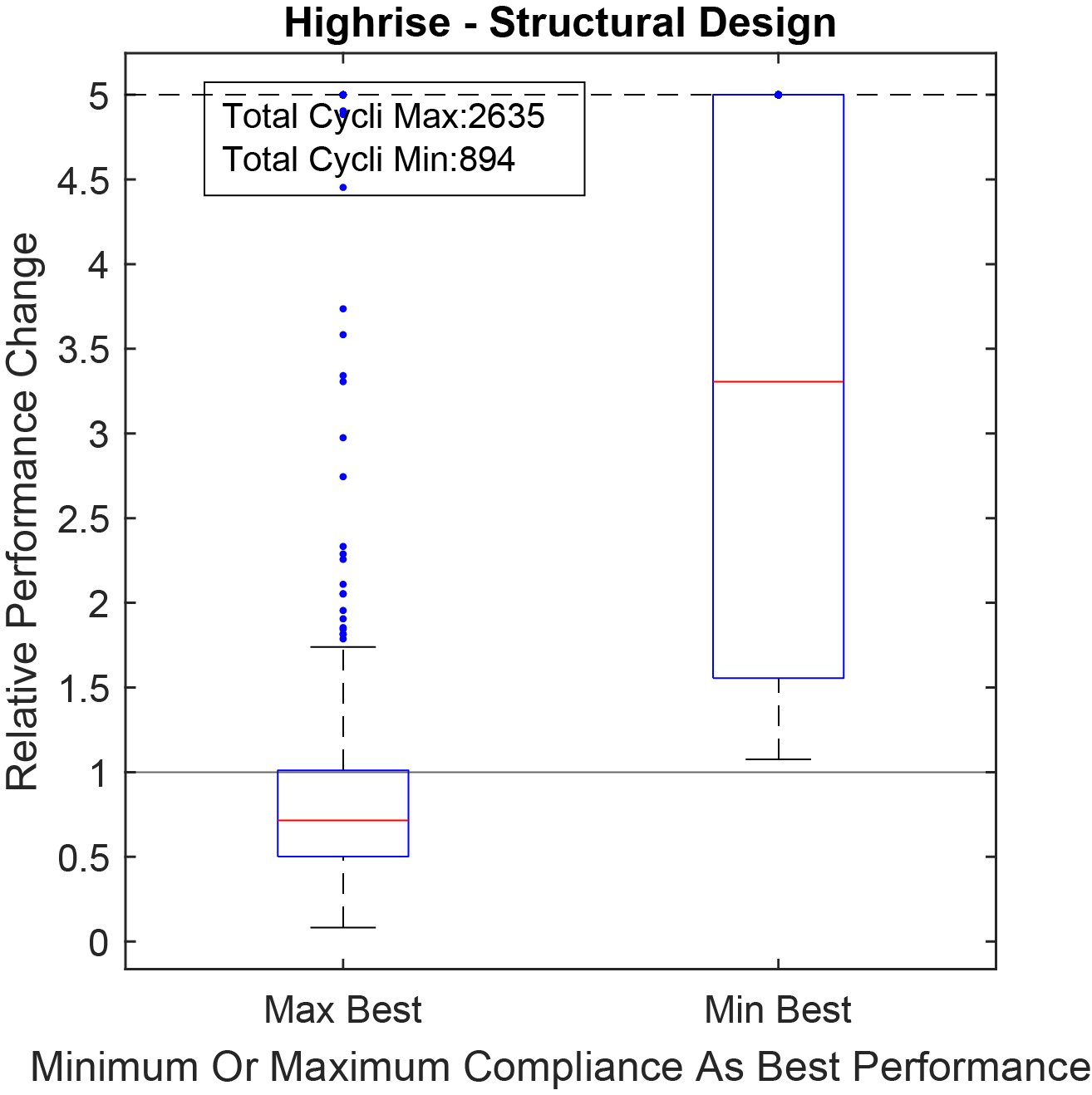
Figure 4: Structural optimization, highest or lowest space strain energy

While some conclusions and results of this study might seem straightforward, it was required to confirm that this procedure is capable of finding improved solutions to single disciplinary problems. This graduation project was developed as contribution to the PhD research from S. Boonstra (Eindhoven University of Technology). 

[1] Horváth, I. (2005). On some crucial issues of computer support of conceptual design (D. Talaba & T. Roche, Eds). Dordrecht: Springer Netherlands.
[2] Akin (2001) Chapter 6 – variants in design cognition. In C.M. Eastman, W.M. Mccracken & W.C. Newsletter 
(Eds), Design knowing and learning: Cognition in design eduation (p.105-124). Oxford: Elsevier Science.
[3] Flage, F., Welle, B., Bansal, P., Soremekun G., & Haymaker, 
J. (2009). Multidisciplinary process integration and design optimization of a classroom  building. Journal of information technology in construction (ITcon), 14(38), 595-612. [4] Hofmeyer, H., Davila Delgado,. J.M. (2015). Coevolutionary and genetic algorithm based building spatial and structural design. Artificial Intelligence for Engineering Design, Analysis and Manufacturing, 29. Boonstra, S., van der Blom, K., Hofmeyer, H., [5] Emmerich, M.T.M., van Schijndel, A.W.M., & de Wilde, P. (2018, 3 20). Toolbox for super-structured and super-structure free multi-disciplinary building spatial design optimization. Advanced Engineering Informatics, 36, 86-100.