Micro Analysis of Strain Hardening Cementitious Composite
Concrete is widely used for civil and structural applications, but to guarantee structural safety, concrete must be reinforced since the material has poor tensile strength, is very brittle and has a relatively low toughness. By reinforcing concrete, the energy that occurs after reaching the peak tensile strength will be absorbed, which reduces further propagation of cracks and hence increases the ductility and toughness of the cementitious composite. The construction industry mainly uses conventional reinforcements, but these are not always applicable. One example will be Three-Dimensional Printed Concrete (3DCP) structures. Due to the manufacturing process and often complex geometry of the structure it is difficult to implement rebars or pre-tensioning cables. One promising solution is to use Engineered Cementitious Composites (ECC) or Strain Hardening Cementitious Composites (SHCC) which are based on micromechanical principles. ECC incorporates fibers within the composite matrix. Based on mechanical properties and financial aspects, PVA fibers are the most promising. Studies have also shown that the flowability and buildability of PVA-ECC is also suitable for 3DCP or 3DP-ECC.
The pseudo-strain hardening properties of ECC is associated to multiple cracking of the brittle matrix subjected to tensile stresses. As a tensile load increases, a crack in the matrix may occur. Once a crack occurs, the load will be shared with crack bridging fibers which transfer the load via their interface back into the matrix. If the bridging fibers transfer sufficient load, the matrix may crack again, and the process is repeated until more fibers complete debonding and pull out or break. This means that there is a relation between the fiber bridging process and cracking. As seen in the Header, the repeating cracking process results in plastic behavior. For discontinuous fiber composites, adequate reinforcement implies that the fibers have a sufficient bond strength and embedment length to take over additional loads shed by the cracked matrix. Otherwise, the fibers will be pulled out before new cracks are formed, resulting in catastrophic brittle failure.
While many studies have been conducted on 3DP-ECC, there are still some points of interest which may contribute to the development of 3DCP. Little research is conducted on the mechanical performance of a single isolated fiber which considers the inclinations or inflections that occur within the matrix composite. Yet, most fibers in 3DP-ECC are inflected or inclined, as displayed in Figure 1. It would be beneficial if the performance of 3DP-ECC could be predicted without performing destructive tests. Getting a better understanding of the relation between fiber orientations and the mechanical performance will contribute to this.
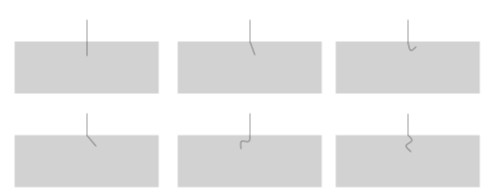
Figure 1: Six examples of fiber orientation at a crack interface
As mentioned, the main function of the fiber is to transfer tensile loads within a crack in the matrix through pull-out. For this research, the goal is to numerically simulate inflected fibers. But before a numerical model can be constructed, the parameters that influence the pull-out behavior must be analysed and understood.
Two mechanical principles are relevant for the stress-displacement relation: bonding and friction. Bonding is the occurrence of physical interaction of the interface between the cementitious matrix and the fiber due to chemical reactions. This relative strong interaction relates to a traction-separation behavior, as schematically displayed in Figure 2. Friction occurs due to the radial stress on the fiber by the shrunken cementitious matrix, as visualised in Figure 3. For PVA-ECC the influence of bonding might be limited due to additional processing of the fibers. Untreated PVA naturally has a strong bond with cementitious composites. This increases the tensile strength but decreases the ductility, which is undesired. To prevent this, the fibers will be coated to prevent chemical bonding. Hence, the main mechanical principle is friction.
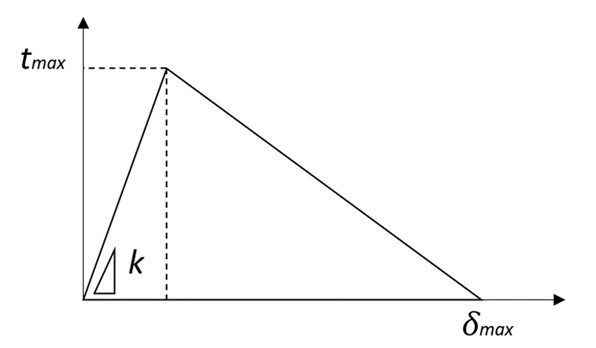
Figure 2: Theoretical model of a traction-separation behavior
To analyse the parameters, multiple laboratory tests must be performed. Parameters of interest for bonding are maximum traction, maximum separation, and the evolution of damage. The friction parameters consider the elastic moduli and Poisson ratios of the materials, matrix shrinkage, the coefficient of friction and the influence of the embedded length.
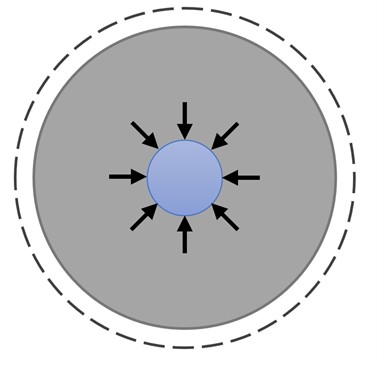
Figure 3: Visualisation of the occurrence of radial stresses on a fiber due to the shrinkage of the surrounding matrix (blue: fiber, grey: matrix, dashed: initial matrix size)
The difficulty for the experimental research is the microscopic scale of the fibers. PVA fibers have a diameter of 40 micrometers and a length of 8 millimeters. The small size and high aspect ratio create challenges. The first challenge is creating specimens. With a maximum embedded length of 4 millimeters a mold must also be small and precise, see Figure 4. The second challenge is the reproducibility of tests for inflected fibers. To solve the challenges, a different strategy will be used; instead of trying to mimic separate specimens, the research accepts that specimens are different. To compensate this, all specimens will be CT-scanned to provide a 3D view of the orientation and inflections of the fiber in the matrix. The results will be copied into a numerical model to verify the input parameters.

Figure 4: Example of a four-parted-mold for creating small specimens (8 by 8 by 4 mm3)
Once the base parameters are known and a numerical working model exists, more variations to the model will be considered. These variations include the porosity, particle distribution and random oriented additional fibers. I hope the research will have two results: the influence of inflections of PVA fibers and a numerical method to analyse any matrix-PVA-fiber composition. This will be one step further in understanding the mechanical behavior of 3DP-ECC.




